Shapes of Atomic Orbitals

s Sublevels are Spherically Shaped

All ℓ = 0 electron waves are s waves, or waves from the s sublevel, and they all describe electrons in s orbitals. As suggested in the previous section, all electron waves from the s sublevel have the same overall shape, regardless of the value of n, regardless of their size, and regardless of the number of nodes they contain. s orbitals always correspond to spherical waves. The quantum numbers n = 1 and ℓ = 0 describe a small spherical wave with no nodes, the quantum numbers n = 2 and ℓ = 0 describe a larger spherical wave with a single node, and the quantum numbers n = 3 and ℓ = 0 describe an even larger spherical wave with two nodes. These waves all look slightly different, as shown in Figure 6.16.

Figure 6.16: Various s orbitals. All of these orbitals have ℓ = 0, but they have different values for n. The first orbital has n = 1, and thus is small and has no nodes. The second orbital has n = 2, and thus is larger and has one node. The third orbital has n = 3, and thus is even larger and has two nodes.

Figure : Notice that the amount of electron density (here represented by the intensity of the blue color) doesn't depend on direction. It does, however, depend on distance from the center of the atom.

Nevertheless, they are all spherical, because they all have ℓ = 0. Their shapes don't change – only their sizes and the number of nodes that they contain.
Now if you think back to an earlier lesson, you might remember something special about the different orientations of a spherical wave. Do you remember what happened when we rotated the spherical wave so that it pointed in different directions? It ended up looking the same, didn't it! No matter which way you rotate a sphere, it always looks the same. So how many different m_l values do you expect for a spherical wave? One, of course! Now that you know spherical waves all have ℓ = 0, you can use your rules for m_l to figure out exactly how many different m_l are allowed. If you look back to Example 4 in the previous lesson, you'll see that we actually did that calculation. It turned out that there was only one allowable value for m_l, and that was m_l = 0. In other words, there is only one orientation of a spherical wave. It all makes sense!
So what does a spherical wave really mean? It means that your probability of finding an electron at any particular distance from the center of the atom only depends on the distance, and not on the direction. You can see this in Figure 6.17.

When the Azimuthal Quantum Number is 1, then m_l Can Only Be -1, 0 or +1

All ℓ = 1 electron waves are p waves, or waves from the p sublevel, and they describe electrons in what are known as p orbitals. Unlike s orbitals, p orbitals are not spherical, so they can have different orientations in space. Now that you know all p orbitals have ℓ = 1, you should be able to figure out exactly how many different p orbital orientations exist by using your rules for m_l. (m_l is the quantum number associated with the orientation of a particular orbital). Let's figure it out.

Example 1 How many different p orbital orientations are possible? Solution: ℓ = 1 From now on, whenever you're told an electron is in a p orbital, you're expected to know that electron has the quantum number ℓ = 1. The question asks how many p orbital orientations are possible, but what it's really asking is how many different ml values are allowed when ℓ = 1. We've already done this type of problem. 1. Find the minimum value of ml. The minimum value of ml is always −ℓ. minimum ml = −1 2. Find the maximum value of ml. The maximum value of ml is always +ℓ maximum ml = +1 3. List all of the integers (no decimals!) starting from the minimum value of ml and ending with the maximum value of ml. ml = −1, 0, 1 In this case ml can equal −1, 0 or 1, so there are a total of 3 allowed values for ml, and thus 3 possible p orbital orientations.

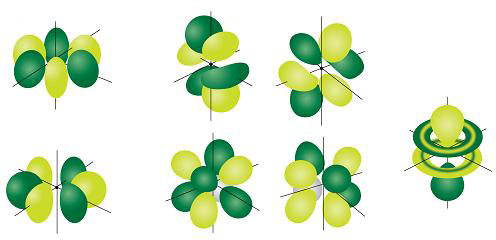
The p Orbitals are Often Described as Dumb-bell Shaped

Even though you know that there are three possible orientations for p orbitals, you can't really predict their shape unless you know a lot more about mathematics, physics, and wave functions. When scientists use the wave function to draw the shape of an electron's p orbital, though, they always end up with is something that looks a lot like a dumb-bell. Not only that, the three different p orbitals (one with m_l = −1, another with m_l = 0, and the third with m_l = 1) turn out to be perpendicular to each other. In other words, if one p orbital points along the x-axis, another p orbital points along the y-axis, and the third points along the z-axis. Scientists typically label these three orbitals p_x, p_y, and p_z respectively. The below figure shows each of the three p orbitals separately, and then all three together on the same atom.

Sometimes we get so caught up thinking about electron wave functions, and electron orbitals, that we forget entirely about the atom itself. Remember, electron standing waves form because electrons get trapped inside an atom by the positive charge on the atom's nucleus. As a result, s orbitals, and p orbitals and even d and f orbitals always extend out from the atom's nucleus. Don't get so caught up in orbitals that you forget where they are and why they exist.
As with s orbitals, p orbitals can be big or small, depending on the value of n, and they can also have more or less nodes, also depending on the value of n. Notice, however, that unlike the s orbital, which can have no nodes at all, a p orbital always has at least one node. Take a look at the p orbital figure above again. Can you spot the node in each of the p orbitals? Since all p orbitals have at least one node, there are no p orbitals with n = 1. In fact, the first principal quantum number, n, for which p orbitals are allowed is n = 2. Of course you could have figured that out for yourself, right? No? Well, here’s a hint – remember the rules for predicting which values of ℓ are allowed for any given value of n. In the last lesson, you learned that ℓ must be no less than 0, but also, no greater than n − 1. For the n = 1 energy level, then, the maximum allowed value for ℓ is:

maximum ℓ = n − 1

maximum ℓ = 1 − 1

maximum ℓ = 0

As a result, only s orbitals (ℓ = 0) are allowed. For the n = 2 energy level, though, the maximum allowed value for ℓ is

maximum ℓ = n − 1

maximum ℓ = 2 − 1

maximum ℓ = 1

which means p orbitals (ℓ = 1) are allowed as well. So now you see that the restrictions on ℓ are actually there to make sure that all n = 1 wave functions have no nodes, all n = 2 wave functions have 1 node, all n = 3 wave functions have 2 nodes, all… well, you get the picture.
One interesting property of p orbitals that is different from s orbitals is that the total amount of electron density changes with both the distance from the center of the atom and the direction. Take a look at Figure 6.18. Notice how the electron density is different depending on which direction you travel from the center of the atom out. In the particular p orbital shown, the probability of finding the electron is greater as you head straight up from the center of the atom than it is as you head straight to the left or to the right of the atom. It turns out that this dependence on direction is very important when it comes to studying how different atoms interact and form bonds. We'll talk more about that in a later chapter.

Figure : For p orbitals, the amount of electron density, and thus the probability of finding an electron, depends on both the distance from the center of the atom and the direction.

The d Orbitals and f Orbitals are Not Easily Visualized

Did you notice how the p orbitals looked a lot fancier than the simple spherical s orbitals? Well, you can imagine that if p orbitals with ℓ = 1 are fancy, then d orbitals, with ℓ = 2 are even fancier, and f orbitals, with ℓ = 3 are just plain crazy! Most people can visualize p orbitals, but d orbitals and f orbitals are actually rather difficult to imagine. Most d orbitals are butterfly shaped, although one has an unusual shape that looks like a doughnut surrounding a Q-tip! The 5 possible d orbitals are shown in Figure 6.19 (and you could have figured out that there were 5, right?). Don't worry too much about why one of the d orbitals is different. Again, it takes a lot of complex math to understand where the different d orbital pictures came from, and you won't have to worry about that unless you decide to go on and study quantum chemistry at the university level. As for f orbitals, they are even hard to draw, not to mention the fact that there are a total of 7 of them (Figure 6.20)! We won't be too concerned with d orbitals in this course, although they do become very important if you want to study certain metals like those found in the center of the periodic table. Similarly, f orbitals aren't all that important when it comes to common chemicals like hydrogen, or oxygen, or even copper. They do become important, though when you want to study some of the most important radioactive elements like uranium and plutonium!

Figure : The probability patterns for the d orbitals.

Figure : The probability patterns for the f orbitals.