Why are copper and chromium exceptions to electron configuration?

 
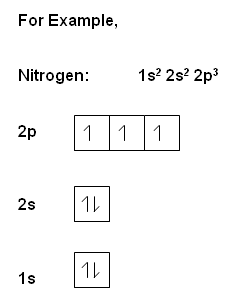
Electronic Configuration of Elements

Mendeleev noticed the recurrence of properties of elements as the atomic weight increased, and he invented the Periodic Table of Element, which is a useful tool for organizing and correlating chemical and physical properties of chemical elements. Today, the most popular Periodic Table form is shaped by results of quantum theory. Quantum theory rationalized the existence of and arrangement of all elements in today's Periodic Table. It has also been applied to explain their chemical properties.

Electronic Configuration of Elements

Skills to develop

• Explain the rules for filling electrons in atomic orbitals -- Pauli exclusion principle and Hund's rule
• Fill electrons in atomic orbitals--Aufbau process
• Explain the arrangement of elements in terms of quantum numbers
• Explain the systematic variation of element properties

Energy Levels in Many-Electron Atoms

In order to fill the electrons in various atomic orbitals, we need to know how the energy levels vary as the nuclear charge increases. For hydrogen-like atoms, the approximate energy levels are as indicated below:


The shielding effect and electron-electron interactions cause the energy levels of subshells such as 2s & 2p to be different from those of H-like atoms. This is done by treating the electron shield cores as a proton but the core has an effective nuclear charge Z.
For the H-like atoms, energy levels for 2s, 2p stay the same, but the separation between 2s and 2p energy levels increases as the atomic number (Z) increases. Similar situations happen for 3s, 3p, and 3d energy levels. The energy diagrams of H, Li & K are used to illustrate this point. The color diagram is from a Hyperion website discussing quantum numbers and structure of atoms

Understand how the energy level vary is the key to the Aufbau process, because Electrons tend to occupy the lowest energy level available. But before we talk about the Aufbau process, we need to be aware of the Pauli exclusion principle and the Hund's rule.

The Pauli Exclusion Principle

The Pauli exclusion principle suggests that only two electrons with opposite spin can occupy an atomic orbital. Stated another way, no two electrons have the same 4 quantum numbers n, l, m, s. Pauli's exclusion principle can be stated in some other ways, but the idea is that energy states have limit room to accommodate electrons. A state accepts two electrons of different spins.
In applying this rule, You should realize that an atomic orbital is an energy state.

Hund's RULE

Hund's rule suggests that electrons prefer parallel spins in separate orbitals of subshells. This rule guides us in assigning electrons to different states in each sub-shell of the atmic orbitals. In other words, electrons fill each and all orbitals in the subshell before they pair up with opposite spins. Pauli exclusion principle and Hund's rule guide us in the aufbau process, which is figuring out the electron configurations for all elements.

The Aufbau Procedure

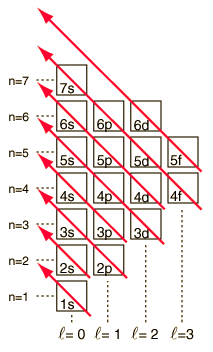
The aufbau procedure (filling order of atomic orbitals) is used to work out the electron confiturations of all atoms. However, modification should be made by applying Hund's rule to be discussed in the next section. The aufbau procedure is based on a rough energy levels diagram of many-electron atoms as shown below:

     7s |~            5d |-----   5f |_______    
                                     Actanides


     6s |_  6p |~~~   5d |=====   4f |=======    
                                     Lanthanides


     5s |_  5p |~~~   4d |-----

                            Note the trend 5s 4d 5p 
                            & develope a pattern

     4s |_  4p |~~~   3d |-----
                         Transition elements

     3s |_  3p |---


     2s |_  2p |---



     1s |-

The fine difference between energy levels cannot be adquately shown.
You've learned various techniques to work out the electronic configurations of elements. Here is yet another form of an energy level diagram:

                                          7p _ _ _
    7s _  5f - - - - - - -  6d ~ ~ ~ ~ ~
                                          6p _ _ _
    6s _  4f - - - - - - -  5d ~ ~ ~ ~ ~

    5s _  4d - - - - -  5p ~ ~ ~

    4s _  3d - - - - -  4p ~ ~ ~

    3s _  3p - - -

    2s _  2p - - -

    1s _

In order to master the technique of the aufbau procedure, you should apply the Hund's rule and Pauli exclusion principle to work out the electronic configuration for closed shells of inert gases. After you worked out, you may compare your result with the following. Do not try to remember it, it is important to know how to work it out.

Z=   2      10     18       36         54           86
    1s2  2s22p6 3s23p6 4s23d104p6 5s24d105p6 6s24f145d106p6
    He      Ne     Ar       Kr         Xe           Rn

Block of elements by highest occupied atomic orbitals

Block of elements by last filled atomic orbitals
1s 2s 3s 4s 5s 6s 7s	4f - - - - - 4f 5f - - - - - 5f	3d - - - 3d 4d - - - 4d 5d - - - 5d 6d - - - 6d	2p - 2p 3p - 3p 4p - 4p 5p - 5p 6p - 6p 7p - 7p

The highest atomic orbitals occupied by electrons determine the properties of the elements. According to this scheme, the periodic table can be divided into s, p, d, and f blocks as seen in the table on the right. This table shows the filling order of atomic orbitals as
1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d 7p The s- and p-blocks of elements are called main group elements. The d-block elements are called transition elements The f-block elements are called the inner transition elements.
In an ordinary periodic table, the s, p, and d block elements are in the main body of the Periodic Table, whereas the f block elements are placed below the main body. If we placed them on the same period where they belong, the Periodic Table would be too long for the screen to accommodate. Thus, we keep the Periodic Table in the usual (long) form.

Special Electronic Configurations

When two electrons occupy the same orbital, they not only have different spins (Pauli exclusion principle), the pairing raises the energy slightly. On the other hand, a half filled subshell and a full filled subshell lower the energy, gaining some stability. Bearing this in mind, you will be able to understand why we have the following special electronic configurations.

Cr [Ar]4s1 3d5	<=All s and d subshells are half full
Cu [Ar]4s1 3d10	<=Prefers a filled d subshell, leaving s with 1
Nb [Kr]5s1 4d4	<=5s and 4d energy levels are close
Mo [Kr]5s1 4d5	similar to Cr above
Tc [Kr]5s2 4d5	(not special, but think of Hund's rule)
Ru [Kr]5s1 4d7	<= Only 1 5s electron
Rh [Kr]5s1 4d8	<= in both
Pd [Kr]5s0 4d10	<= Note filled 4d and empty 5s
Ag [Kr]5s1 4d10	<= partial filled 5s, but filled d

For CHEM120 students, you are not required to remember the special ones, but you should take notice of the electronic configurations of Cr and Cu to realize the gaining of stability due to half and full filled subshells.

Confidence Building Questions

• For the H-like atom, which subshell has the highest energy level?
  4f, 3d, 2p, 1s
  Skill:
  Describe the energy levels of hydrogen atoms.
• For an element with atomic number 20, which is the last or highest occupied subshell of atomic orbitals?
  1s 2s 2p 3s 3p 3d 4s 5s
  Discussion:
  The element is Calcium, Ca.
• How many electrons are required to fill all the following sub shells?
  1s 2s 2p 3s 3p 4s 3d 4p
  Discussion:
  The element is Krypton, Kr.
• Which of the following two electronic configuration is more stable?
  a [Ar]4s¹ 3d⁵
  b [Ar]4s² 3d⁴
  Discussion:
  Check the electronic configuration for Cu and Cr.
• Which of the following two electronic configurations is more stable?
  a [Ar]4s² 3d⁹
  b [Ar]4s¹ 3d¹⁰
  Discussion:
  This is the electronic configuration for copper.
• Choose the electronic configuration for palladium, Pd (Z = 46).
  a [Kr]5s¹ 4d⁷
  b [Kr]5s¹ 4d⁸
  c [Kr]5s⁰ 4d¹⁰
  d [Kr]5s¹ 4d¹⁰

Electron Configuration Anomalies

Electron Configuration Anomalies

• Some of the elements have electron configurations that differ slightly from what our general procedure would lead us to predict. Because a few of these elements are important elements, it is useful to know their actual electron configurations. Six of these are listed on the table below. 

  
  

  
  
  
  
  

  Unusual Electron Configurations

  Element	Predicted Electron Configuration	Actual Electron Configuration
  copper, Cu	[Ar] 3d9 4s2	[Ar] 3d10 4s1
  silver, Ag	[Kr] 4d9 5s2	[Kr] 4d10 5s1
  gold, Au	[Xe] 4f14 5d9 6s2	[Xe] 4f14 5d10 6s1
  palladium, Pd	[Kr] 4d8 5s2	[Kr] 4d10
  chromium, Cr	[Ar] 3d4 4s2	[Ar] 3d5 4s1
  molybdenum, Mo	[Kr] 4d4 5s2	[Kr] 4d5 5s1

Filling Electron Shells

Filling Electron Shells

When an atom or ion receives electrons into its orbitals, the orbitals and shells fill up in a particular manner.

Aufbau principle

You may consider an atom as being "built up" from a naked nucleus by gradually adding to it one electron after another, until all the electrons it will hold have been added. Much as one fills up a container with liquid from the bottom up, the orbitals of an atom are filled from the lowest energy orbitals to the highest energy orbitals.
Orbitals with the lowest principal quantum number () have the lowest energy and will fill up first. Within a shell, there may be several orbitals with the same principal quantum number. In that case, more specific rules must be applied. For example, the three p orbitals of a given shell all occur at the same energy level. So, how are they filled up? ans: all the three p orbitals have same energy so while filling the p orbitals we can fill any one of the Px, Py or Pz first. it is a convention that we chose to fill Px first ,then Py and then Pz for our simplicity. Hence you can opt for filling these three orbitals from right to left also.

Hund's Rule

According to Hund's rule, orbitals of the same energy are each filled with one electron before filling any with a second. Also, these first electrons have the same spin.




This rule is sometimes called the "bus seating rule". As people load onto a bus, each person takes his own seat, sitting alone. Only after all the seats have been filled will people start doubling up.

Pauli Exclusion principle

No two electrons can have all four quantum numbers the same. What this translates to in terms of our picture of orbitals is that each orbital can only hold two electrons, one "spin up" (+½) and one "spin down" (-½).

This animation demonstrates the Aufbau principle, Hund's Rule, and the Pauli Exclusion principle.

Orbital Order

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, 8s.
Although this looks confusing, there is an easy way to remember.

Understanding the above rules and diagrams will allow you to determine the electron configuration of almost any atom or ion.

How to Write the Electron Configuration of an Isolated Atom

Wikipedia has related information at Electron configuration

Electron-configuration notation is relatively straightforward. An isolated Calcium atom, for example, would have configuration of 1s²2s²2p⁶3s²3p⁶4s² in its ground state. Other configurations like 1s²2s²2p⁶3s²3p⁶4s¹4p¹ are possible, but these excited states have a higher energy. They are not stable and generally only exist for a brief moment.
The ground state configuration for Ca could be abbreviated by using the preceding noble gas (the elements found all the way on the right of the periodic table) as [Ar]4s², where Ar is argon.
Noble gases have very stable configurations, and are extremely reluctant to lose or gain electrons. Noble gas atoms are also the only ones regularly found as isolated atoms in the ground state. Atoms of other elements all undergo bonding under the conditions that we live under and this affects the orbitals that the outermost electrons are in. In that sense the electron configurations for the other elements are somewhat hypothetical: to encounter an isolated atom of, say, tungsten (W), we would have to first vaporize a metal that boils at 5800K. However, knowing atomic configurations is useful because it does help us to understand how and why they bond, i.e. why and how they change the configuration of their outer valence electrons.

Rule of Stability

A subshell is particularly stable if it is half full or full. Given two configurations, the atom would "choose" the more stable one.
Example: In the following configuration, Cu: [Ar]4s²3d⁹, copper's d shell is just one away from stability, and therefore, one electron from the s shell jumps into the d shell: [Ar]4s¹3d¹⁰. This way, the d shell is full, and is therefore stable, and the s shell is half full, and is also stable.





Another example: Chromium has a configuration of [Ar]4s¹3d⁵, although you would expect to see four d electrons instead of five. This is because an s electron has jumped into the d orbital, giving the atom two half-full shells—much more stable than a d orbital with only four electrons.
The stability rule applies to atoms in the same group as chromium and copper.
If one of these atoms has been ionized, that is, it loses an electron, it will come from the s orbital rather than the d orbital. For instance, the configuration of Cu⁺ is [Ar]4s⁰3d¹⁰. If more electrons are removed, they will come from the d orbital.

Magnetism

The spin of an electron creates a magnetic field (albeit ridiculously weak), so unpaired electrons create a small magnetic field. Paired electrons have opposite spin, so the magnetic fields cancel each other out, leading to diamagnetism.

Magnetism is a well-known effect. Chances are, you have magnets on your refrigerator. As you already know, only certain elements are magnetic. Electron configurations help to explain why.
Diamagnetism is actually a very weak repulsion to magnetic fields. All elements have diamagnetism to some degree. It occurs when there are paired electrons.
Paramagnetism is an attraction to external magnetic fields. It is also very weak. It occurs whenever there is an unpaired electron in an orbital.
Both diamagnetism and paramagnetism are responses of spins acting independently from each other. This leads to rather weak repulsion and attraction respectively. However, when they are located in a solid they may also interact with each other and respond collectively and that can lead to rather different properties:
Ferromagnetism is the permanent magnetism that we encounter in our daily lives. It occurs when all the unpaired spins in a solid couple and tend to align themselves in the same direction, leading to a strong attraction when exposed to a magnetic field. This only occurs at room temperature with three elements: iron (Fe), nickel (Ni), and cobalt (Co). Gadolinium (Gd) is a borderline case. It loses its ferromagnetism at 20^oC; above that temperature the spins start to act alone. However, there are many alloys and compounds that exhibit strong ferromagnetic coupling. The strongest one is Nd₂Fe₁₄B
Antiferromagnetism is also a permanent magnetism in which unpaired spins align, but they do so in opposite directions. The result is that the material does not react very strongly to a magnetic field at all. Chromium (Cr) is an example.
'Ferrimagnetism is a combination of ferro- and antiferromagetism. Unpaired spins align partly in opposite directions, but the compensation is not complete. This is why the material is still attracted strongly to a magnetic field. Magnetite Fe₃O₄ is such a substance. It was the first material studied for its magnetic properties and may well be the one sitting on your fridge.

Order of Filling of Electron States

As the periodic table of the elements is built up by adding the necessary electrons to match the atomic number, the electrons will take the lowest energy consistent with the Pauli exclusion principle. The maximum population of each shell is determined by the quantum numbers and the diagram at left is one way to illustrate the order of filling of the electron energy states. For a single electron, the energy is determined by the principal quantum n number and that quantum number is used to indicate the "shell" in which the electrons reside. For a given shell in multi-electron atoms, those electrons with lower orbital quantum number l will be lower in energy because of

The electron configuration for any element may be found by clicking on that element in the periodic table. The first exception to the above scheme that is encountered is chromium, where the fifth 3d electron state is occupied instead of the second 4s state

Shapes of Atomic Orbitals

s Sublevels are Spherically Shaped

All ℓ = 0 electron waves are s waves, or waves from the s sublevel, and they all describe electrons in s orbitals. As suggested in the previous section, all electron waves from the s sublevel have the same overall shape, regardless of the value of n, regardless of their size, and regardless of the number of nodes they contain. s orbitals always correspond to spherical waves. The quantum numbers n = 1 and ℓ = 0 describe a small spherical wave with no nodes, the quantum numbers n = 2 and ℓ = 0 describe a larger spherical wave with a single node, and the quantum numbers n = 3 and ℓ = 0 describe an even larger spherical wave with two nodes. These waves all look slightly different, as shown in Figure 6.16.

Figure 6.16: Various s orbitals. All of these orbitals have ℓ = 0, but they have different values for n. The first orbital has n = 1, and thus is small and has no nodes. The second orbital has n = 2, and thus is larger and has one node. The third orbital has n = 3, and thus is even larger and has two nodes.

Figure : Notice that the amount of electron density (here represented by the intensity of the blue color) doesn't depend on direction. It does, however, depend on distance from the center of the atom.

Nevertheless, they are all spherical, because they all have ℓ = 0. Their shapes don't change – only their sizes and the number of nodes that they contain.
Now if you think back to an earlier lesson, you might remember something special about the different orientations of a spherical wave. Do you remember what happened when we rotated the spherical wave so that it pointed in different directions? It ended up looking the same, didn't it! No matter which way you rotate a sphere, it always looks the same. So how many different m_l values do you expect for a spherical wave? One, of course! Now that you know spherical waves all have ℓ = 0, you can use your rules for m_l to figure out exactly how many different m_l are allowed. If you look back to Example 4 in the previous lesson, you'll see that we actually did that calculation. It turned out that there was only one allowable value for m_l, and that was m_l = 0. In other words, there is only one orientation of a spherical wave. It all makes sense!
So what does a spherical wave really mean? It means that your probability of finding an electron at any particular distance from the center of the atom only depends on the distance, and not on the direction. You can see this in Figure 6.17.

When the Azimuthal Quantum Number is 1, then m_l Can Only Be -1, 0 or +1

All ℓ = 1 electron waves are p waves, or waves from the p sublevel, and they describe electrons in what are known as p orbitals. Unlike s orbitals, p orbitals are not spherical, so they can have different orientations in space. Now that you know all p orbitals have ℓ = 1, you should be able to figure out exactly how many different p orbital orientations exist by using your rules for m_l. (m_l is the quantum number associated with the orientation of a particular orbital). Let's figure it out.

Example 1 How many different p orbital orientations are possible? Solution: ℓ = 1 From now on, whenever you're told an electron is in a p orbital, you're expected to know that electron has the quantum number ℓ = 1. The question asks how many p orbital orientations are possible, but what it's really asking is how many different ml values are allowed when ℓ = 1. We've already done this type of problem. 1. Find the minimum value of ml. The minimum value of ml is always −ℓ. minimum ml = −1 2. Find the maximum value of ml. The maximum value of ml is always +ℓ maximum ml = +1 3. List all of the integers (no decimals!) starting from the minimum value of ml and ending with the maximum value of ml. ml = −1, 0, 1 In this case ml can equal −1, 0 or 1, so there are a total of 3 allowed values for ml, and thus 3 possible p orbital orientations.

The p Orbitals are Often Described as Dumb-bell Shaped

Even though you know that there are three possible orientations for p orbitals, you can't really predict their shape unless you know a lot more about mathematics, physics, and wave functions. When scientists use the wave function to draw the shape of an electron's p orbital, though, they always end up with is something that looks a lot like a dumb-bell. Not only that, the three different p orbitals (one with m_l = −1, another with m_l = 0, and the third with m_l = 1) turn out to be perpendicular to each other. In other words, if one p orbital points along the x-axis, another p orbital points along the y-axis, and the third points along the z-axis. Scientists typically label these three orbitals p_x, p_y, and p_z respectively. The below figure shows each of the three p orbitals separately, and then all three together on the same atom.

Sometimes we get so caught up thinking about electron wave functions, and electron orbitals, that we forget entirely about the atom itself. Remember, electron standing waves form because electrons get trapped inside an atom by the positive charge on the atom's nucleus. As a result, s orbitals, and p orbitals and even d and f orbitals always extend out from the atom's nucleus. Don't get so caught up in orbitals that you forget where they are and why they exist.
As with s orbitals, p orbitals can be big or small, depending on the value of n, and they can also have more or less nodes, also depending on the value of n. Notice, however, that unlike the s orbital, which can have no nodes at all, a p orbital always has at least one node. Take a look at the p orbital figure above again. Can you spot the node in each of the p orbitals? Since all p orbitals have at least one node, there are no p orbitals with n = 1. In fact, the first principal quantum number, n, for which p orbitals are allowed is n = 2. Of course you could have figured that out for yourself, right? No? Well, here’s a hint – remember the rules for predicting which values of ℓ are allowed for any given value of n. In the last lesson, you learned that ℓ must be no less than 0, but also, no greater than n − 1. For the n = 1 energy level, then, the maximum allowed value for ℓ is:

maximum ℓ = n − 1

maximum ℓ = 1 − 1

maximum ℓ = 0

As a result, only s orbitals (ℓ = 0) are allowed. For the n = 2 energy level, though, the maximum allowed value for ℓ is

maximum ℓ = n − 1

maximum ℓ = 2 − 1

maximum ℓ = 1

which means p orbitals (ℓ = 1) are allowed as well. So now you see that the restrictions on ℓ are actually there to make sure that all n = 1 wave functions have no nodes, all n = 2 wave functions have 1 node, all n = 3 wave functions have 2 nodes, all… well, you get the picture.
One interesting property of p orbitals that is different from s orbitals is that the total amount of electron density changes with both the distance from the center of the atom and the direction. Take a look at Figure 6.18. Notice how the electron density is different depending on which direction you travel from the center of the atom out. In the particular p orbital shown, the probability of finding the electron is greater as you head straight up from the center of the atom than it is as you head straight to the left or to the right of the atom. It turns out that this dependence on direction is very important when it comes to studying how different atoms interact and form bonds. We'll talk more about that in a later chapter.

Figure : For p orbitals, the amount of electron density, and thus the probability of finding an electron, depends on both the distance from the center of the atom and the direction.

The d Orbitals and f Orbitals are Not Easily Visualized

Did you notice how the p orbitals looked a lot fancier than the simple spherical s orbitals? Well, you can imagine that if p orbitals with ℓ = 1 are fancy, then d orbitals, with ℓ = 2 are even fancier, and f orbitals, with ℓ = 3 are just plain crazy! Most people can visualize p orbitals, but d orbitals and f orbitals are actually rather difficult to imagine. Most d orbitals are butterfly shaped, although one has an unusual shape that looks like a doughnut surrounding a Q-tip! The 5 possible d orbitals are shown in Figure 6.19 (and you could have figured out that there were 5, right?). Don't worry too much about why one of the d orbitals is different. Again, it takes a lot of complex math to understand where the different d orbital pictures came from, and you won't have to worry about that unless you decide to go on and study quantum chemistry at the university level. As for f orbitals, they are even hard to draw, not to mention the fact that there are a total of 7 of them (Figure 6.20)! We won't be too concerned with d orbitals in this course, although they do become very important if you want to study certain metals like those found in the center of the periodic table. Similarly, f orbitals aren't all that important when it comes to common chemicals like hydrogen, or oxygen, or even copper. They do become important, though when you want to study some of the most important radioactive elements like uranium and plutonium!

Figure : The probability patterns for the d orbitals.

Figure : The probability patterns for the f orbitals.

 

Quantum Numbers and Atomic Orbitals

Quantum Numbers and Atomic Orbitals

By solving the Schrödinger equation (Hy = Ey), we obtain a set of mathematical equations, called wave functions (y), which describe the probability of finding electrons at certain energy levels within an atom.
A wave function for an electron in an atom is called an atomic orbital; this atomic orbital describes a region of space in which there is a high probability of finding the electron. Energy changes within an atom are the result of an electron changing from a wave pattern with one energy to a wave pattern with a different energy (usually accompanied by the absorption or emission of a photon of light).
Each electron in an atom is described by four different quantum numbers. The first three (n, l, m_l) specify the particular orbital of interest, and the fourth (m_s) specifies how many electrons can occupy that orbital.
 

1. Principal Quantum Number (n):  n = 1, 2, 3, …, ∞
   Specifies the energy of an electron and the size of the orbital (the distance from the nucleus of the peak in a radial probability distribution plot). All orbitals that have the same value of n are said to be in the same shell (level). For a hydrogen atom with n=1, the electron is in its ground state; if the electron is in the n=2 orbital, it is in an excited state. The total number of orbitals for a given n value is n².

2. Angular Momentum (Secondary, Azimunthal) Quantum Number (l):  l = 0, ..., n-1.
   Specifies the shape of an orbital with a particular principal quantum number. The secondary quantum number divides the shells into smaller groups of orbitals called subshells (sublevels). Usually, a letter code is used to identify l to avoid confusion with n:

l	0	1	2	3	4	5	...
Letter	s	p	d	f	g	h	...

The subshell with n=2 and l=1 is the 2p subshell; if n=3 and l=0, it is the 3s subshell, and so on. The value of l also has a slight effect on the energy of the subshell; the energy of the subshell increases with l (s < p < d < f).

3. Magnetic Quantum Number (m_l):  m_l = -l, ..., 0, ..., +l.
   Specifies the orientation in space of an orbital of a given energy (n) and shape (l). This number divides the subshell into individual orbitals which hold the electrons; there are 2l+1 orbitals in each subshell. Thus the s subshell has only one orbital, the p subshell has three orbitals, and so on.

4. Spin Quantum Number (m_s):  m_s = +½ or -½.
   Specifies the orientation of the spin axis of an electron. An electron can spin in only one of two directions (sometimes called up and down).
   The Pauli exclusion principle (Wolfgang Pauli, Nobel Prize 1945) states that no two electrons in the same atom can have identical values for all four of their quantum numbers. What this means is that no more than two electrons can occupy the same orbital, and that two electrons in the same orbital must have opposite spins.
   Because an electron spins, it creates a magnetic field, which can be oriented in one of two directions. For two electrons in the same orbital, the spins must be opposite to each other; the spins are said to be paired. These substances are not attracted to magnets and are said to be diamagnetic. Atoms with more electrons that spin in one direction than another contain unpaired electrons. These substances are weakly attracted to magnets and are said to be paramagnetic.

Table of Allowed Quantum Numbers

n	l	ml	Number of orbitals	Orbital Name	Number of electrons
1	0	0	1	1s	2
2	0	0	1	2s	2
	1	-1, 0, +1	3	2p	6
3	0	0	1	3s	2
	1	-1, 0, +1	3	3p	6
	2	-2, -1, 0, +1, +2	5	3d	10
4	0	0	1	4s	2
	1	-1, 0, +1	3	4p	6
	2	-2, -1, 0, +1, +2	5	4d	10
	3	-3, -2, -1, 0, +1, +2, +3	7	4f	14

 
 

Writing Electron Configurations

The distribution of electrons among the orbitals of an atom is called the electron configuration. The electrons are filled in according to a scheme known as the Aufbau principle ("building-up"), which corresponds (for the most part) to increasing energy of the subshells:

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f

It is not necessary to memorize this listing, because the order in which the electrons are filled in can be read from the periodic table in the following fashion:
 

 
Or, to summarize:

 
In electron configurations, write in the orbitals that are occupied by electrons, followed by a superscript to indicate how many electrons are in the set of orbitals (e.g., H 1s¹)
Another way to indicate the placement of electrons is an orbital diagram, in which each orbital is represented by a square (or circle), and the electrons as arrows pointing up or down (indicating the electron spin). When electrons are placed in a set of orbitals of equal energy, they are spread out as much as possible to give as few paired electrons as possible (Hund's rule).

examples will be added at a later date

In a ground state configuration, all of the electrons are in as low an energy level as it is possible for them to be. When an electron absorbs energy, it occupies a higher energy orbital, and is said to be in an excited state.
 
 

Properties of Monatomic Ions

The electrons in the outermost shell (the ones with the highest value of n) are the most energetic, and are the ones which are exposed to other atoms. This shell is known as the valence shell. The inner, core electrons (inner shell) do not usually play a role in chemical bonding.
Elements with similar properties generally have similar outer shell configurations. For instance, we already know that the alkali metals (Group I) always form ions with a +1 charge; the "extra" s¹ electron is the one that's lost:

IA	Li	1s22s1	Li+	1s2
	Na	1s22s22p63s1	Na+	1s22s22p6
	K	1s22s22p63s23p64s1	K+	1s22s22p63s23p6

The next shell down is now the outermost shell, which is now full — meaning there is very little tendency to gain or lose more electrons. The ion's electron configuration is the same as the nearest noble gas — the ion is said to be isoelectronic with the nearest noble gas. Atoms "prefer" to have a filled outermost shell because this is more electronically stable.

• The Group IIA and IIIA metals also tend to lose all of their valence electrons to form cations.

IIA	Be	1s22s2	Be2+	1s2
	Mg	1s22s22p63s2	Mg2+	1s22s22p6
IIIA	Al	1s22s22p63s23p1	Al3+	1s22s22p6

• The Group IV and V metals can lose either the electrons from the p subshell, or from both the s and p subshells, thus attaining a pseudo-noble gas configuration.

IVA	Sn	[Kr]4d105s25p2	Sn2+	[Kr]4d105s2
			Sn4+	[Kr]4d10
	Pb	[Xe]4f145d106s26p2	Pb2+	[Xe]4f145d106s2
			Pb4+	[Xe]4f145d10
VA	Bi	[Xe]4f145d106s26p3	Bi3+	[Xe]4f145d106s2
			Bi5+	[Xe]4f145d10

• The Group IV - VII non-metals gain electrons until their valence shells are full (8 electrons).

IVA	C	1s22s22p2	C4-	1s22s22p6
VA	N	1s22s22p3	N3-	1s22s22p6
VIA	O	1s22s22p4	O2-	1s22s22p6
VIIA	F	1s22s22p5	F-	1s22s22p6

• The Group VIII noble gases already possess a full outer shell, so they have no tendency to form ions.

VIIIA	Ne	1s22s22p6
	Ar	1s22s22p63s23p6

• Transition metals (B-group) usually form +2 charges from losing the valence s electrons, but can also lose electrons from the highest d level to form other charges.

B-group	Fe	1s22s22p63s23p63d64s2	Fe2+	1s22s22p63s23p63d6
			Fe3+	1s22s22p63s23p63d5

Atomic Sub Shells

• Atoms have electrons arranged in definite energy levels. The electrons within the first quantum shell are closest to the nucleus and have the lowest energies.
• Subsequent energy levels further away from the nucleus have higher energies.
• The shells are labelled by assigning each one a principal number, n, where n = 1, 2, 3…
• Evidence for electrons being arranged in energy levels is given by atomic spectroscopy and successive ionisation energy values.

• The energy levels are evident due to the large increase in ionisation energies after the removal of certain electrons.
• The number of electrons allowed in one energy level can be summarised by the formula 2n² where n = energy level quantum number.
• Within energy levels in atoms, there are also sub energy levels, or orbitalss.
• The orbitals are labelled s, p, d and f. In the first energy level, there is only one orbital (s). The second shell has two orbitals (s and p), the third three (s, p, d) and the fourth has four (s, p, d, f).
• The different orbitals can hold a different number of electrons:
  • 1 s orbital can hold 2
  • 3 p orbitals can hold 6
  • 5 d orbitals can hold 10
  • 7 f orbitals can hold 14
• This explains why the total number of electrons in each energy level is 2n².

• The sub shells can be summarised in the diagram below, notice that the n=3 and n=4 sub shells overlap.

Atomic Orbitals

• The s, p, d and f s orbitals compose of regions of space where the electrons can be found.

• Electrons within the same orbitals have the same amount of energy.
• The electrons do not lie within a specific place within an orbital, but can be found anywhere around the orbital.
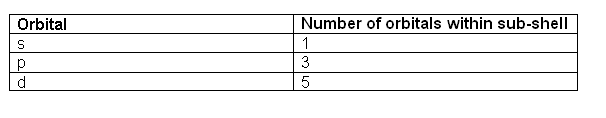
• Each atomic orbital can contain 2 electrons, which can spin in two directions , the electrons within the same orbital spin in opposite directions.
• To describe accurately the state of an electron, you need to be able to state:
  1. The electron shell it is in (1, 2, 3, 4….)
  2. The orbital it is in within the electron shell (s, p, d, f)
  3. Its spin.

Filling the orbitals

• The arrangement of electrons within an atom, is referred to as the electronic configuration of an atom.
• The orbitals are filled within a definite order to produce the lowest energy arrangement available.
• The lowest energy levels are always filled first.
• Where there is more than one orbital within the same energy, the separate orbitals are filled separately with the same spin (think of bus analogy, i.e. people will aim to sit on their own seat on the bus, but when the seats are full, they will be forced to sit on a seat with someone else!). Then the electrons pair up in orbitals.